由地基变形参数计算Winkler-Pasternak系数
Winkler – Pasternak系数C1和C2可应用若干刚性条基放置在Winkler – Pasternak弹性地基上形成的刚度矩阵方程计算。矩阵方程为:
Edef | - | 变形模量 [MPa] |
ν | - | 泊松比 |
Eoed | - | 压缩模量 [MPa] |
G | - | 剪切模量 [MPa] |
以上参数中, Edef 和 ν 是相互独立的, Edef 和Eoed ,G相互转换关系如下:
![]()
且
![]()
对条形基础,有效范围取宽度方向 2b 和 变形范围为基底以下 H深度
基于弹性路基假设求解位移和条基荷载间的关系:
![]()
其中 P 是柔度矩阵.
基于基础下各向同性弹性地层且无水平位移的假设,柔度矩阵 P 可简化为:

其中
![]()
且
![]()
对于双系数温克尔地基模型, 柔度矩阵 P 可表达为:
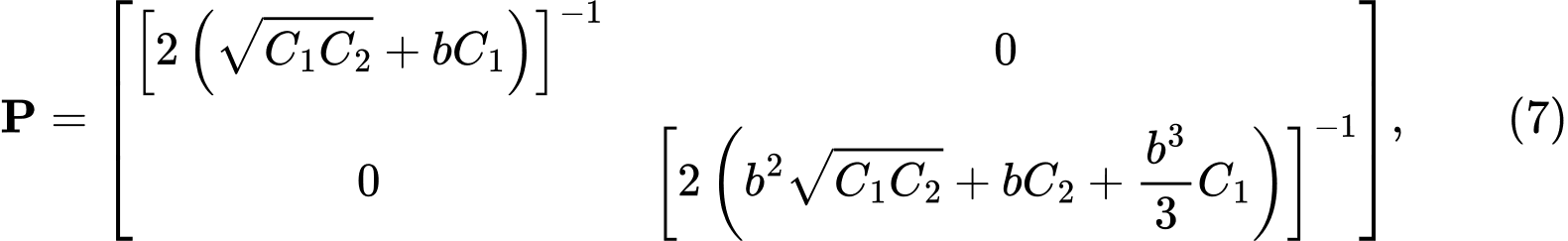
其中 C1, C2 温克尔地基系数. 对比柔度矩阵 P 表达(4)和 (7),由一致性可得:
![]()
且
![]()
其中

且
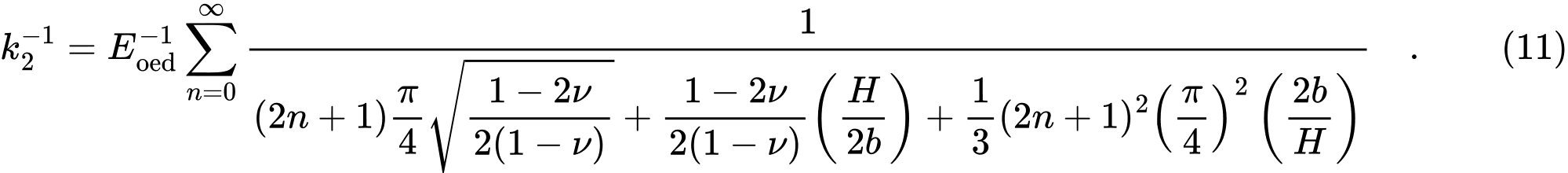
通过式 (8) 和 (9), 可计算得到 C1 , C2。式(10)和(11)无穷累加中,GEO5计算时取前21项以简化计算并确保足够的精度。
参考文献:
Kuklík, P.: Příspěvek k řešení vrstevnatého podloží, Pozemní stavby, 7-1984