Surface utile
Pour résoudre le problème des fondations subissant des charges excentriques, le programme propose deux options pour traiter des dimensions efficaces de la surface de la fondation :
- la surface utile est supposée de forme rectangulaire
- la surface utile est supposée de forme générique
Forme rectangulaire
Une solution simplifiée est utilisée dans de tels cas. En cas d'excentricité axiale (le moment de flexion n'agit que dans un seul plan), le calcul suppose une répartition uniforme de la contrainte de contact σ appliquée uniquement sur une partie de la fondation l1, qui est deux fois moins grande que l'excentricité e par rapport à la longueur totale l.
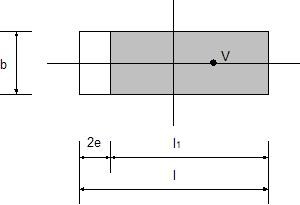 Détermination de la surface utile en cas d'excentricité axiale
Détermination de la surface utile en cas d'excentricité axiale
L'aire de la surface efficace (b*l1) est admise pour calculer la contrainte de contact, de sorte que cette dernière s'exprime de la façon suivante :
![]()
En cas de charge excentrée générique (la fondation est chargée par la force verticale V et par les moments de flexion M1 et M2), la charge est remplacée par une force unique avec les excentricités données :
![]()
![]()
L'aire de la surface efficace découle de la condition selon laquelle la force V doit agir de manière excentrée :
![]()
Forme générique de la contrainte de contact
En cas de charge excentrée, la surface utile est déterminée en partant du principe que la force résultante V doit agir au centre de gravité de la zone comprimée. La figure ci-dessous illuste la solution théorique du problème :
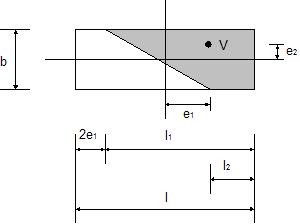 Détermination de la contrainte de contact - cas d'une excentricité et d'une forme génériques
Détermination de la contrainte de contact - cas d'une excentricité et d'une forme génériques
En raison de la complexité considérable pour déterminer la position exacte de l’axe neutre, ce qui est décisif pour le calcul de la surface utile, le programme suit la solution proposée par Highter a Anders1), dans laquelle les zones utiles sont calculées à l’aide de graphiques.
1) Highter, W.H. - Anders, J.C.: Dimensioning Footings Subjected to Eccentric Loads Journal of Geotechnical Engineering. ASCE, Vol. 111, No GT5, pp 659 - 665